Como Sacar La Magnitud De Un Triangulo

Z 50 al ser un ángulo llano. Sean a y h dos lados conocidos del triángulo a3 h5.

Como Calcular Los Angulos De Un Triangulo Dados Sabiendo Conociendo Sus Lados Teorema Del Coseno 6 Youtube

Por ejemplo 5 al cuadrado más 12 al cuadrado es 169.

Como sacar la magnitud de un triangulo. Cuando ves la ecuación puedes pensar en esto como la longitud del lado a multiplicada por sí misma mas la longitud del lado b multiplicada por sí misma es igual a la longitud de c multiplicada por sí misma. Así para encontrar LM todo lo que necesitamos hacer es dividir LN entre 2. Dividimos entre -2 toda la ecuación.

Sea 0AxA un triángulo rectángulo observemos que 0A es la hipotenusa. Según la propiedad de los triángulos 20wz. Para calcular la magnitud o módulo de un vector A A x A y conociendo sus coordenadas se utiliza la siguiente formula.

Se presentan varios ejemplos donde se conocen todas las medidas del triángulo o cuando se desconoce una de ellas un cateto o hipotenusa. Para que puedas visualizarlo lo fórmula es la siguiente. Como encontrar las razones trigonométricas fundamentales seno coseno y tangente para un ángulo dado en un triángulo rectángulo.

Hay varias formas de comprobar la fórmula de Pitágoras pero las dos más sencillas son las siguientes. Identificar la operación que representa ½bh en este caso es multiplicación. Reordena la ecuación del teorema de Pitágoras para calcular la magnitud.

Sustituimos con los datos de las coordenadas que tenemos y desarrollamos. Al aplicar el teorema de Pitágoras tenemos. Si es una mediana del triángulo encuentre la longitud de.

Para obtener la BASE de un triángulo con un área de 20ft 2 y una altura de 4ft. Hipotenusa b lado faltante por Pitágoras. Entonces el lado faltante es.

Basta trazar por cada uno de los vértices del triángulo paralelas al vector dado. Magnitud de los lados del triangulo. Step 1 Recuerda la fórmula para el área de un triángulo.

El teorema de Pitágoras establece que A 2 B 2 C 2 siendo A y B los componentes horizontal y vertical del triángulo y C la hipotenusa. Para lo cual se hace uso del teorema de pitágoras. También debes conocer el valor de la longitud de un lado así que asigna ese valor a b.

El lado opuesto a este ángulo se conoce como hipotenusa otro nombre para el lado más largo. En este caso ya conoces el área así que asigna ese valor a A. Solo resta unir los puntos trasladados.

Intentemos el Teorema de Pitágoras con un triángulo. Supongamos que se desea medir la magnitud RfXYZ que es función de otras magnitudes XYZ que. Y los podemos obtener despejando la fórmula veamos los pasos siguientes de cómo hacerlo.

A² b² c² con a y b siendo los lados más cortos y c siendo el más largo. Un triángulo rectángulo tiene un ángulo que mide 90 grados. V x 2 y 2.

-3mc y ion 3. Se repite el proceso por C y se obtiene C. La longitud de la hipotenusa se puede descubrir usando el teorema de Pitágoras pero para descubrir los otros dos lados se debe usar el seno y el coseno.

El hecho de que sea una mediana nos dice que M debe ser un punto medio de. Este número será la magnitud del vector. Sí sobre este círculo tomamos un punto Px y el radio OP genera un ángulo positivo de magnitud t radianes como se muestra.

X 2 y 2 v 2. Puede usar el teorema de Pitágoras para encontrar un valor para la longitud de c la hipotenusa. Las tres medidas forman un triángulo y su rampa recta es la hipotenusa del mismo.

Por lo tanto 20w50 w30. Magnitud de los lados del triangulo GeoGebra. Si no conoces el área.

Cálculo de la incertidumbre de una medida indirecta Una vez obtenida la incertidumbre de las medidas directas calculamos las de las medidas indirectas. Como puede usted ver el teorema de Pitágoras es muy práctico para calcular la magnitud de uno de los lados de un triángulo rectángulo cuando se conocen sus otros dos lados. Y 30 59 180.

Utiliza el número que acabas de calcular como a y la coordenada z para z y calcula la raíz cuadrada de a 2 z 2. Por lo tanto la magnitud del vector es de 13. Si tienes al menos dos lados del triángulo conocidos puedes conseguir el faltante aplicando el teorema de Pitágoras.

Como la hipotenusa es el vector tienes que resolver la ecuación para hallar el valor de C. En este video se ven algunos ejemplos de cómo. Dado un triángulo y un vector A A trasladar el triángulo dado.

A A x 2 A y 2 Esta expresión es una aplicación del Teorema de Pitágoras. Un círculo con centro en el origen de coordenadas y de radio la unidad es llamado círculo unitario. 0A 2 A x 2 A y 2.

Magnitud de los lados del triangulo. Pero cómo fue que Pitágoras hace más de 2500 años encontró esta fórmula tan útil. Hola buenas tardes Carlos Julián solo tengo una tres iones Ion1.

La longitud de una rampa se refiere a su altura y al largo de la superficie debajo de ella. Por A se trazará entonces una paralela a AB que al intersectar con la paralela que pasa por B arroja B. Se conviene que se generan ángulos positivos si son medidos a partir del eje x y girando en el sentido.

En el ejercicio 3. 102 10 10. Dejar la variable del valor que queremos buscar en este caso la b y pasar el.

5mc y me dice que entre el ion 1 y el dos hay una distancia 110-6 m y entre el ion 2 y 3 hay una distancia de 110-6 m me pide calcular la fuerza entre los iones 1 y 3 mi duda es aplico directo la ley de coulomb usan do Q1 y Q3 y sumo 110-6 m 110-6 m y lo elevo al cuadrado o tendria que sacar. Ahora ángulos opuesto equivalen lo mismo por lo tanto el triángulo te quedaría. Como dicha mediana pasa por los puntos y usamos la fórmula de la ecuación de la recta dados dos puntos.

En la figura mostrada LN 14 unidades NK 22 unidades y KL 34 unidades. Que dice que la hipotenusa al cuadrado es igual a la suma de sus catetos al cuadrado. La raíz cuadrada de 169 es 13.

Multiplicamos por 7 y despejamos. Como tenemos división de fracciones lo anterior es equivalente a. Según el Teorema de Pitágoras el cuadrado de la longitud de la rampa equivale a la suma de los cuadrados de los otros dos lados del triángulo.

Deberemos entonces tomar 5 y 12 y calcular el cuadrado de ambos 25 y 144 y sumar esos resultados. La fórmula para el área de un triángulo es A12bh1 X Fuente de investigación A área del triángulo b longitud de la base del triángulo h altura de la base del triánguloStep 2 Mira el triángulo y determina qué variables conoces.

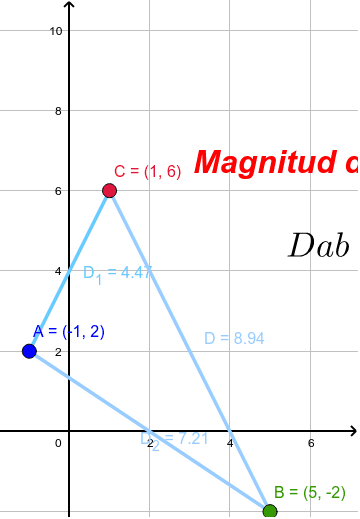
Magnitud De Los Lados Del Triangulo Geogebra